Category Archives: LaganLighter

ParaGrapher: A Parallel and Distributed Graph Loading Library for Large-Scale Compressed Graphs – BigData’25 (Short Paper)

Posted on by


DOI:

Whereas the literature describes an increasing number of graph algorithms, loading graphs remains a time-consuming component of the end-to-end execution time. Graph frameworks often rely on custom graph storage formats, that are not optimized for efficient loading of large-scale graph datasets. Furthermore, graph loading is often not optimized as it is time-consuming to implement.

This shows a demand for high-performance libraries capable of efficiently loading graphs to (i) accelerate designing new graph algorithms, (ii) to evaluate the contributions across a wide range of graph datasets, and (iii) to facilitate easy and fast comparisons across different graph frameworks.

We present ParaGrapher, a library for loading large-scale compressed graphs in parallel and distributed graph frameworks. ParaGrapher supports (a) loading the graph while the caller is blocked and (b) interleaving graph loading with graph processing. ParaGrapher is designed to support loading graphs in shared-memory, distributed-memory, and out-of-core graph processing.

We explain the design of ParaGrapher and present a performance model of graph decompression. Our evaluation shows that ParaGrapher delivers up to 3.2 times speedup in loading and up to 5.2 times speedup in end-to-end execution (i.e., through interleaved loading and execution).

Source Code

https://github.com/DIPSA-QUB/ParaGrapher

API Documentation

Please refer to the Wiki, https://github.com/DIPSA-QUB/ParaGrapher/wiki/API-Documentation, or download the PDF file using https://github.com/DIPSA-QUB/ParaGrapher/raw/main/doc/api.pdf .

BibTex

@articel{paragrapher-bigdata,

}

Related Posts & Source Code

ParaGrapher Web Page

On Optimizing Locality of Graph Transposition on Modern Architectures

Posted on by

DOI: 10.48550/arXiv.2501.06872
PDF version

This paper investigates the shared-memory Graph Transposition (GT) problem, a fundamental graph algorithm that is widely used in graph analytics and scientific computing.


Previous GT algorithms have significant memory requirements that are proportional to the number of vertices and threads which obstructs their use on large graphs. Moreover, atomic memory operations have become comparably fast on recent CPU architectures, which creates new opportunities for improving the performance of concurrent atomic accesses in GT.

We design PoTra, a GT algorithm which leverages graph structure and processor and memory architecture to optimize locality and performance. PoTra limits the size of additional data structures close to CPU cache sizes and utilizes the skewed degree distribution of graph datasets to optimize locality and performance. We present the performance model of PoTra to explain the connection between cache and memory response times and graph locality.


Our evaluation of PoTra on three CPU architectures and 20 real-world and synthetic graph datasets with up to 128 billion edges demonstrates that PoTra achieves up to 8.7 times speedup compared to previous works and if there is a performance loss it remains limited to 15.7%, on average.

Source code

The source code of PoTra is available on LaganLighter repository.

BibTex

@misc{PoTra,
     title={On Optimizing Locality of Graph Transposition on Modern Architectures}, 
     author={Mohsen {Koohi Esfahani} and Hans Vandierendonck},
     year={2025},
     eprint={2501.06872},
     archivePrefix={arXiv},
     primaryClass={cs.DC},
     url={https://arxiv.org/abs/2501.06872},
     doi={10.48550/arXiv.2501.06872} 
}


LaganLighter

Accelerating Loading WebGraphs in ParaGrapher

Posted on by

PDF version
DOI: 10.48550/arXiv.2507.00716

ParaGrapher is a graph loading API and library that enables graph processing frameworks to load large-scale compressed graphs with minimal overhead. This capability accelerates the design and implementation of new high-performance graph algorithms and their evaluation on a wide range of graphs and across different frameworks.

However, our previous study identified two major limitations in ParaGrapher: inefficient utilization of high-bandwidth storage and reduced decompression bandwidth due to increased compression ratios. To address these limitations, we present two optimizations for ParaGrapher in this paper.

To improve storage utilization, particularly for high-bandwidth storage, we introduce ParaGrapher-FUSE (PG-Fuse) a filesystem based on the FUSE (Filesystem in User Space). PG-Fuse optimizes storage access by increasing the size of requested blocks, reducing the number of calls to the underlying filesystem, and caching the received blocks in memory for future calls.

To improve the decompression bandwidth, we introduce CompBin, a compact binary representation of the CSR format. CompBin facilitates direct accesses to neighbors while preventing storage usage for unused bytes.

Our evaluation on 12 real-world and synthetic graphs with up to 128 billion edges shows that PG-Fuse and CompBin achieve up to 7.6 and 21.8 times speedup, respectively.

Source Code

https://github.com/DIPSA-QUB/ParaGrapher

API Documentation

Please refer to the Wiki, https://github.com/DIPSA-QUB/ParaGrapher/wiki/API-Documentation, or download the PDF file using https://github.com/DIPSA-QUB/ParaGrapher/raw/main/doc/api.pdf .

BibTex

@misc{pg_fuse,
      title={Accelerating Loading WebGraphs in ParaGrapher}, 
      author={Mohsen {Koohi Esfahani}},
      year={2025},
      eprint={2507.00716},
      archivePrefix={arXiv},
      primaryClass={cs.DC},
      url={https://arxiv.org/abs/2507.00716}, 
}

Related Posts & Source Code

ParaGrapher Web Page

Random Vertex Relabelling in LaganLighter

Posted on by

To evaluate the impacts of locality-optimizing reordering algorithms, a baseline is required. To create the baseline a random assignment of IDs to vertices may be used to produce a representation of the graph with reduced locality [ DOI:10.1109/ISPASS57527.2023.00029, DOI:10.1109/IISWC53511.2021.00020 ].

To that end, we create the random_ordering() function in relabel.c file. It consists a number of iterations. In each iteration, concurrent threads traverse the list of vertices and assign them new IDs. The function uses xoshiro to produce random numbers.

The alg4_randomize tests this function for a number of graphs. For each dataset, an initial plot of degree distribution of Neighbor to Neighbor Average ID Distance (N2N AID) [DOI:10.1109/IISWC53511.2021.00020] is created. Also, after each iteration of random_ordering() the N2N AID distribution is plotted. This shows the impacts of randomization.

The complete results for all graphs can be seen in this PDF file. The results for some graphs are in the following.

The algorithm has been executed on a machine with two AMD 7401 CPUs, 128 cores, 128 threads. The report created by the launcher is in the following.

Technical Posts


LaganLighter

Minimum Spanning Forest of MS-BioGraphs

Posted on by

We use MASTIFF to compute the weight of Minimum Spanning Forest (MST) of MS-BioGraphs while ignoring self-edges of the graphs.

– MS1

Using machine with 24 cores.

MSF weight: 109,915,787,546

– MS50

Using machine with 128 cores.

MSF weight: 416,318,200,808

MS-BioGraphs
Related Posts

Technical Posts


LaganLighter

Topology-Based Thread Affinity Setting (Thread Pinning) in OpenMP

Posted on by

In applications such as graph processing, it is important how threads are pinned on CPU cores as the threads that share resources (such as memory and cache) can accelerate the performance by processing consecutive blocks of input dataset, especially, when the dataset has a high-level of locality.

In LaganLighter, we read the CPU topology to specify how OpenMP threads are pinned. In omp.c file, the block starting with comment “Reading sibling groups of each node“, reads the “/sys/devices/system/cpu/cpu*/topology/thread_siblings” files to identify the sibling threads and three arrays ("node_sibling_groups_start_ID“, “sibling_group_cpus_start_offsets“, and “sibling_groups_cpus“) are used to store the sibling CPUs.

Then, in block starting with comment “Setting affinity of threads“, the sibling groups are read and based on the total number of threads requested by user, a number of threads with consecutive IDs are pinned to sibling CPUs.

For a machine with 24 cores, 48 hyperthreads, when 48 threads are requested, we have:

If 96 threads are created, we have:

Technical Posts


LaganLighter

Selective Parallel Loading of Large-Scale Compressed Graphs with ParaGrapher – arXiv Version

Posted on by

PDF version
DOI: 10.48550/arXiv.2404.19735

Comprehensive evaluation is one of the basis of experimental science. In High-Performance Graph Processing, a thorough evaluation of contributions becomes more achievable by supporting common input formats over different frameworks. However, each framework creates its specific format, which may not support reading large-scale real-world graph datasets. This shows a demand for high-performance libraries capable of loading graphs to (i) accelerate designing new graph algorithms, (ii) to evaluate the contributions on a wide range of graph algorithms, and (iii) to facilitate easy and fast comparison over different graph frameworks.

To that end, we present ParaGrapher, a high-performance API and library for loading large-scale and compressed graphs. ParaGrapher supports different types of requests for accessing graphs in shared- and distributed-memory and out-of-core graph processing. We explain the design of ParaGrapher and present a performance model of graph decompression, which is used for evaluation of ParaGrapher over three storage types.

Our evaluation shows that by decompressing compressed graphs in WebGraph format, ParaGrapher delivers up to 3.2 times speedup in loading and up to 5.2 times speedup in end-to-end execution in comparison to the binary and textual formats.

ParaGrapher is available online on https://blogs.qub.ac.uk/DIPSA/ParaGrapher/.

Source Code

https://github.com/DIPSA-QUB/ParaGrapher

API Documentation

Please refer to the Wiki, https://github.com/DIPSA-QUB/ParaGrapher/wiki/API-Documentation, or download the PDF file using https://github.com/DIPSA-QUB/ParaGrapher/raw/main/doc/api.pdf .

BibTex

@misc{paragrapher-arxiv,
  title = { Selective Parallel Loading of Large-Scale 
            Compressed Graphs with {ParaGrapher}}, 
  author = { {Mohsen} {Koohi Esfahani} and Marco D'Antonio and 
             Syed Ibtisam Tauhidi and Thai Son Mai and 
             Hans Vandierendonck},
  year = {2024},
  eprint = {2404.19735},
  archivePrefix = {arXiv},
  primaryClass = {cs.AR},
  doi = {10.48550/arXiv.2404.19735},
  url={https://arxiv.org/abs/2404.19735}, 
}

Related Posts & Source Code

ParaGrapher Web Page

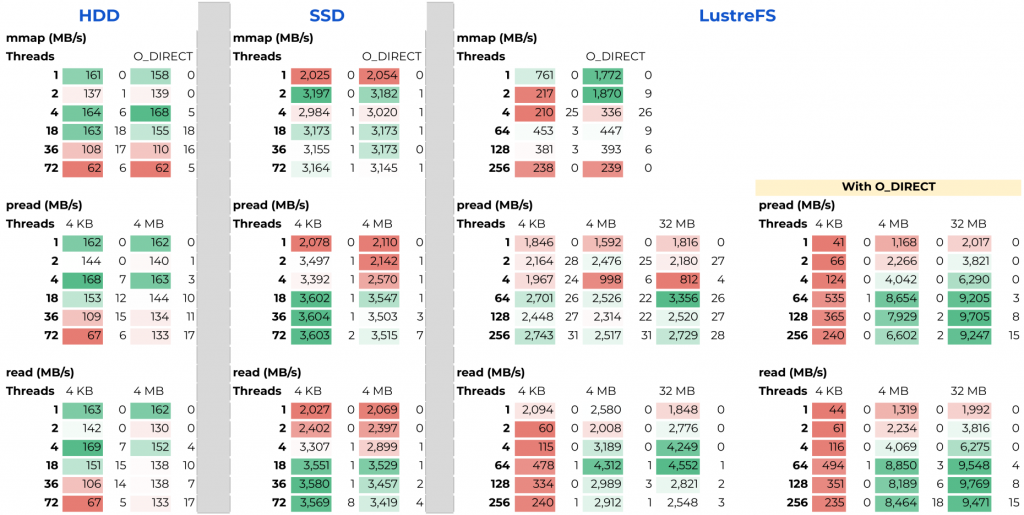
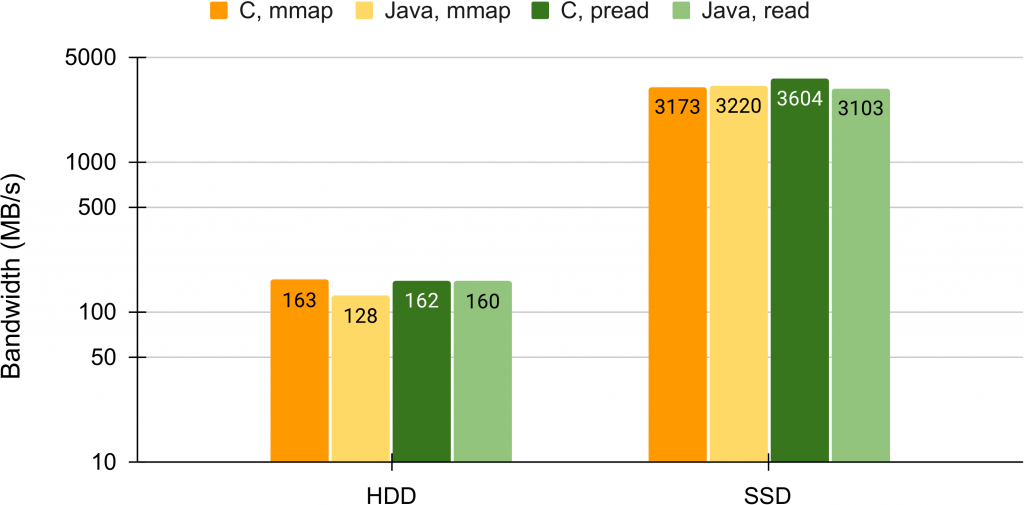
An Evaluation of Bandwidth of Different Storage Types (HDD vs. SSD vs. LustreFS) for Different Block Sizes and Different Parallel Read Methods (mmap vs pread vs read)

Posted on by

Short URL of this post: https://blogs.qub.ac.uk/DIPSA/HDD-vs-SSD-vs-LustreFS-2024

We evaluate read bandwidth of three storage types:

  • HDD: A 6TB Hitachi HUS726060AL 7200RPM SATA v3.1
  • SSD: A 4TB Samsung MZQL23T8HCLS-00A07 PCIe4 NVMe v1.4
  • LustreFS: A parallel file system with total 2PB with a SSD pool

and for three parallel read methods:

and for two block sizes:

  • 4 KB blocks
  • 4 MB blocks

The source code is available on ParaGrapher repository:

The OS cache of storage contents have been dropped after each evaluation
(sudo sh -c 'echo 3 >/proc/sys/vm/drop_caches').
The flushcache.c file (https://github.com/DIPSA-QUB/ParaGrapher/blob/main/test/flushcache.c) can be used with the same functionality for users without sudo access, however, it usually takes more time to be finished.

For LustreFS, we have repeated the evaluation of read and pread using O_DIRECT flag as this flag prevents client-side caching.

For HDD and SSD experiments, we have used a machine with Intel W-2295 3.00GHz CPU, 18 cores, 36 hyper-threads, 24MB L3 cache, 256 GB DDR4 2933Mhz memory, running Debian 12 Linux 6.1. For LustreFS, we have used a machine with 2TB 3.2GHz DDR4 memory, 2 AMD 7702 CPUs, in total, 128 cores, 256 threads.

The results of the evaluation using read_bandwidth.c are in the following table. The values are Bandwidth in MB/s. Also, 1-2 digits close to each number with a white background are are percentage of load imbalance between parallel threads.

Please click on the image to expand.

C vs. Java

We measure the bandwidth of SSD and HDD in C (mmap and pread) vs. Java (mmap and read). We use a machine with Intel W-2295 3.00GHz CPU, 18 cores, 36 hyper-threads, 24MB L3 cache, 256 GB DDR4 2933Mhz memory, running Debian 12 Linux 6.1 and the following codes:

The results are in the following.


For similar comparisons you may refer to:
– https://github.com/david-slatinek/c-read-vs.-mmap/tree/main
– https://eklausmeier.goip.de/blog/2016/02-03-performance-comparison-mmap-versus-read-versus-fread/

Technical Posts


ParaGrapher

ParaGrapher Integrated to LaganLighter

Posted on by

ParaGrapher source code has been integrated to LaganLighter and access to different WebGraph formats are available in LaganLighter:

  • PARAGRAPHER_CSX_WG_400_AP
  • PARAGRAPHER_CSX_WG_404_AP
  • PARAGRAPHER_CSX_WG_800_AP

For further details, please refer to
– LaganLighter source coder Repository: https://github.com/DIPSA-QUB/LaganLighter, particularly, the graph.c file.
– ParaGrapher source code repository: https://github.com/DIPSA-QUB/ParaGrapher particularly, the src/webgraph.c and src/WG*.java files.

Read more about ParaGrapher and LaganLighter.

Related Posts

ParaGrapher


LaganLighter

ParaGrapher Source Code For WebGraph Types

Posted on by

ParaGrapher source code for accessing WebGraphs have been published. The supported graph types are:

ParaGrapher uses its asynchronous and parallel API to implement these graph types. The user needs to implement a callback function that is called by the API upon completion of reading a block of edges. Poplar uses a shared memory for interaction between its C library and the Java library that deploys the WebGraph framework.

For further details, please refer to Poplar source code repository: https://github.com/DIPSA-QUB/ParaGrapher, particularly, src/webgraph.c and src/WG*.java files.

ParaGrapher

Related Posts