Category Archives: LaganLighter

Random Vertex Relabelling in LaganLighter

Posted on by
Reply

To evaluate the impacts of locality-optimizing reordering algorithms, a baseline is required. To create the baseline a random assignment of IDs to vertices may be used to produce a representation of the graph with reduced locality [ DOI:10.1109/ISPASS57527.2023.00029, DOI:10.1109/IISWC53511.2021.00020 ].

To that end, we create the random_ordering() function in relabel.c file. It consists a number of iterations. In each iteration, concurrent threads traverse the list of vertices and assign them new IDs. The function uses xoshiro to produce random numbers.

The alg4_randomize tests this function for a number of graphs. For each dataset, an initial plot of degree distribution of Neighbor to Neighbor Average ID Distance (N2N AID) [DOI:10.1109/IISWC53511.2021.00020] is created. Also, after each iteration of random_ordering() the N2N AID distribution is plotted. This shows the impacts of randomization.

The complete results for all graphs can be seen in this PDF file. The results for some graphs are in the following.

The algorithm has been executed on a machine with two AMD 7401 CPUs, 128 cores, 128 threads. The report created by the launcher is in the following.

Technical Posts


LaganLighter

Minimum Spanning Forest of MS-BioGraphs

Posted on by
Reply

We use MASTIFF to compute the weight of Minimum Spanning Forest (MST) of MS-BioGraphs while ignoring self-edges of the graphs.

– MS1

Using machine with 24 cores.

MSF weight: 109,915,787,546

– MS50

Using machine with 128 cores.

MSF weight: 416,318,200,808

MS-BioGraphs
Related Posts

Technical Posts


LaganLighter

Topology-Based Thread Affinity Setting (Thread Pinning) in OpenMP

Posted on by

In applications such as graph processing, it is important how threads are pinned on CPU cores as the threads that share resources (such as memory and cache) can accelerate the performance by processing consecutive blocks of input dataset, especially, when the dataset has a high-level of locality.

In LaganLighter, we read the CPU topology to specify how OpenMP threads are pinned. In omp.c file, the block starting with comment “Reading sibling groups of each node“, reads the “/sys/devices/system/cpu/cpu*/topology/thread_siblings” files to identify the sibling threads and three arrays ("node_sibling_groups_start_ID“, “sibling_group_cpus_start_offsets“, and “sibling_groups_cpus“) are used to store the sibling CPUs.

Then, in block starting with comment “Setting affinity of threads“, the sibling groups are read and based on the total number of threads requested by user, a number of threads with consecutive IDs are pinned to sibling CPUs.

For a machine with 24 cores, 48 hyperthreads, when 48 threads are requested, we have:

If 96 threads are created, we have:

Technical Posts


LaganLighter

Selective Parallel Loading of Large-Scale Compressed Graphs with ParaGrapher – arXiv Version

Posted on by
Reply

PDF version
DOI: 10.48550/arXiv.2404.19735

Comprehensive evaluation is one of the basis of experimental science. In High-Performance Graph Processing, a thorough evaluation of contributions becomes more achievable by supporting common input formats over different frameworks. However, each framework creates its specific format, which may not support reading large-scale real-world graph datasets. This shows a demand for high-performance libraries capable of loading graphs to (i) accelerate designing new graph algorithms, (ii) to evaluate the contributions on a wide range of graph algorithms, and (iii) to facilitate easy and fast comparison over different graph frameworks.

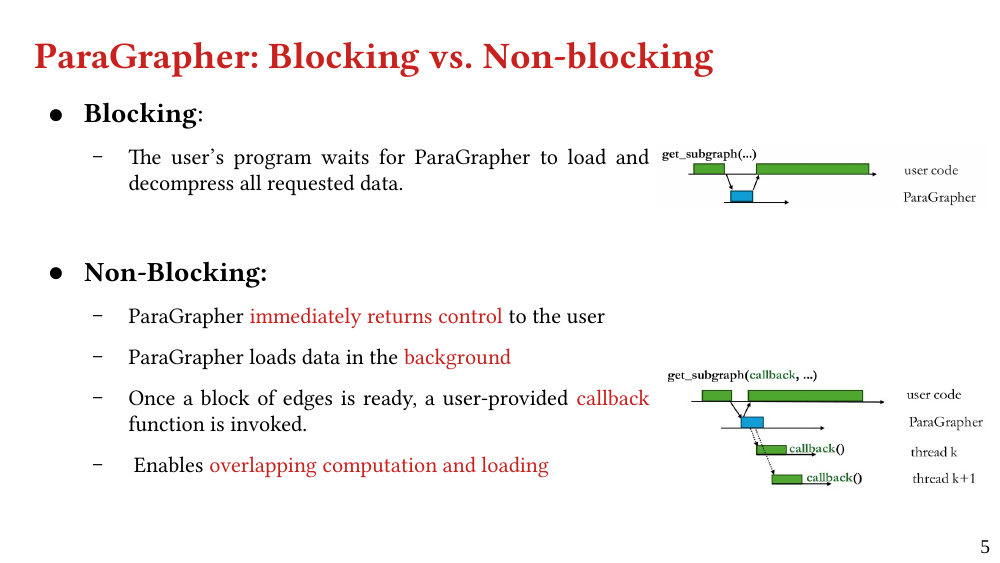
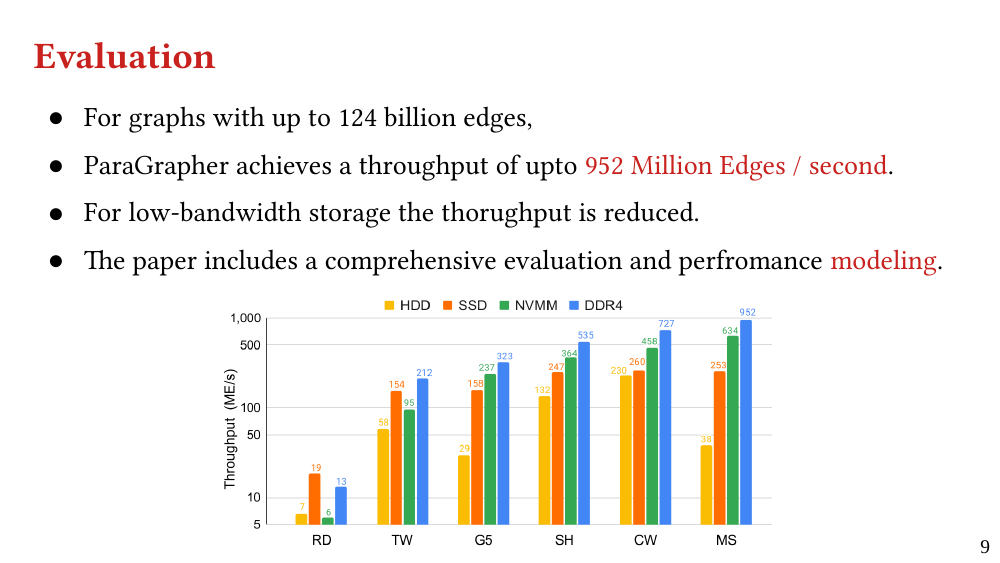
To that end, we present ParaGrapher, a high-performance API and library for loading large-scale and compressed graphs. ParaGrapher supports different types of requests for accessing graphs in shared- and distributed-memory and out-of-core graph processing. We explain the design of ParaGrapher and present a performance model of graph decompression, which is used for evaluation of ParaGrapher over three storage types.

Our evaluation shows that by decompressing compressed graphs in WebGraph format, ParaGrapher delivers up to 3.2 times speedup in loading and up to 5.2 times speedup in end-to-end execution in comparison to the binary and textual formats.

ParaGrapher is available online on https://blogs.qub.ac.uk/DIPSA/ParaGrapher/.

BibTex

@misc{paragrapher-arxiv,
  title = { Selective Parallel Loading of Large-Scale 
            Compressed Graphs with ParaGrapher}, 
  author = { {Mohsen} {Koohi Esfahani} and Marco D'Antonio and 
             Syed Ibtisam Tauhidi and Thai Son Mai and 
             Hans Vandierendonck},
  year = {2024},
  eprint = {2404.19735},
  archivePrefix = {arXiv},
  primaryClass = {cs.AR},
  doi = {10.48550/arXiv.2404.19735}
}

Related Posts & Source Code

ParaGrapher Web Page

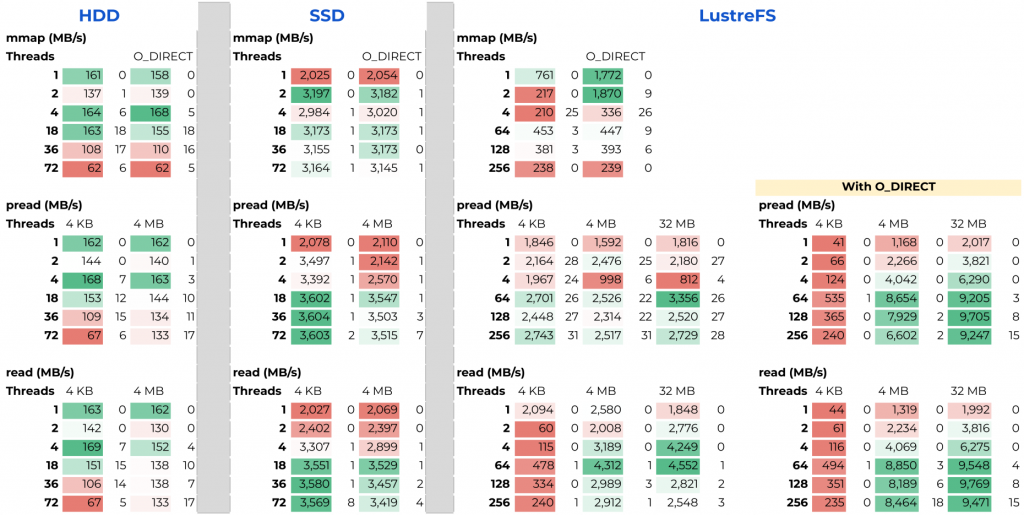
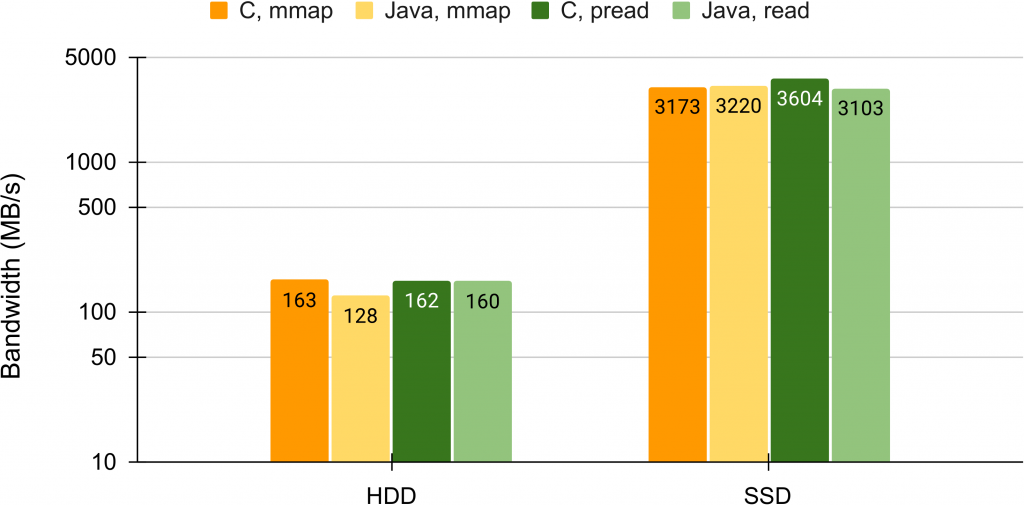
An Evaluation of Bandwidth of Different Storage Types (HDD vs. SSD vs. LustreFS) for Different Block Sizes and Different Parallel Read Methods (mmap vs pread vs read)

Posted on by
Reply

Short URL of this post: https://blogs.qub.ac.uk/DIPSA/HDD-vs-SSD-vs-LustreFS-2024

We evaluate read bandwidth of three storage types:

  • HDD: A 6TB Hitachi HUS726060AL 7200RPM SATA v3.1
  • SSD: A 4TB Samsung MZQL23T8HCLS-00A07 PCIe4 NVMe v1.4
  • LustreFS: A parallel file system with total 2PB with a SSD pool

and for three parallel read methods:

and for two block sizes:

  • 4 KB blocks
  • 4 MB blocks

The source code is available on ParaGrapher repository:

The OS cache of storage contents have been dropped after each evaluation
(sudo sh -c 'echo 3 >/proc/sys/vm/drop_caches').
The flushcache.c file (https://github.com/DIPSA-QUB/ParaGrapher/blob/main/test/flushcache.c) can be used with the same functionality for users without sudo access, however, it usually takes more time to be finished.

For LustreFS, we have repeated the evaluation of read and pread using O_DIRECT flag as this flag prevents client-side caching.

For HDD and SSD experiments, we have used a machine with Intel W-2295 3.00GHz CPU, 18 cores, 36 hyper-threads, 24MB L3 cache, 256 GB DDR4 2933Mhz memory, running Debian 12 Linux 6.1. For LustreFS, we have used a machine with 2TB 3.2GHz DDR4 memory, 2 AMD 7702 CPUs, in total, 128 cores, 256 threads.

The results of the evaluation using read_bandwidth.c are in the following table. The values are Bandwidth in MB/s. Also, 1-2 digits close to each number with a white background are are percentage of load imbalance between parallel threads.

Please click on the image to expand.

C vs. Java

We measure the bandwidth of SSD and HDD in C (mmap and pread) vs. Java (mmap and read). We use a machine with Intel W-2295 3.00GHz CPU, 18 cores, 36 hyper-threads, 24MB L3 cache, 256 GB DDR4 2933Mhz memory, running Debian 12 Linux 6.1 and the following codes:

The results are in the following.


For similar comparisons you may refer to:
– https://github.com/david-slatinek/c-read-vs.-mmap/tree/main
– https://eklausmeier.goip.de/blog/2016/02-03-performance-comparison-mmap-versus-read-versus-fread/

Technical Posts


ParaGrapher

ParaGrapher Integrated to LaganLighter

Posted on by
Reply

Poplar source code has been integrated to LaganLighter and access to different WebGraph formats are available in LaganLighter:

  • PARAGRAPHER_CSX_WG_400_AP
  • PARAGRAPHER_CSX_WG_404_AP
  • PARAGRAPHER_CSX_WG_800_AP

For further details, please refer to
– LaganLighter source coder Repository: https://github.com/DIPSA-QUB/LaganLighter, particularly, the graph.c file.
– ParaGrapher source code repository: https://github.com/DIPSA-QUB/ParaGrapher particularly, the src/webgraph.c and src/WG*.java files.

Read more about ParaGrapher and LaganLighter.

Related Posts

ParaGrapher Source Code For WebGraph Types

Posted on by
Reply

ParaGrapher source code for accessing WebGraphs have been published. The supported graph types are:

ParaGrapher uses its asynchronous and parallel API to implement these graph types. The user needs to implement a callback function that is called by the API upon completion of reading a block of edges. Poplar uses a shared memory for interaction between its C library and the Java library that deploys the WebGraph framework.

For further details, please refer to Poplar source code repository: https://github.com/DIPSA-QUB/ParaGrapher, particularly, src/webgraph.c and src/WG*.java files.

ParaGrapher

Related Posts

On Designing Structure-Aware High-Performance Graph Algorithms (PhD Thesis)

Posted on by
Reply

Mohsen Koohi Esfahani
Supervisors: Hans Vandierendonck and Peter Kilpatrick

Thesis in PDF format
Thesis on QUB Pure Portal

Graph algorithms find several usages in industry, science, humanities, and technology. The fast-growing size of graph datasets in the context of the processing model of the current hardware has resulted in different bottlenecks such as memory locality, work-efficiency, and load-balance that degrade the performance. To tackle these limitations, high-performance computing considers different aspects of the execution in order to design optimized algorithms through efficient usage of hardware resources.

The main idea in this thesis is to analyze the structure of graphs to exploit special features that are key to introduce new graph algorithms with optimized performance.

First, we study the structure of real-world graph datasets with skewed degree distribution and the applicability of graph relabeling algorithms as the main restructuring tools to improve performance and memory locality. To that end, we introduce novel locality metrics including Cache Miss Rate Degree Distribution, Effective Cache Size, Push Locality and Pull Locality, and Degree Range Decomposition.

Based on this structural analysis, we introduce the Uniform Memory Demands strategy that (i) recognizes diverse memory demands and behaviours as a source of performance inefficiency, (ii) separates contrasting memory demands into groups with uniform behaviours across each group, and (iii) designs bespoke data structures and algorithms for each group in order to satisfy memory demands with the lowest overhead.

We apply the Uniform Memory Demands strategy to design three graph algorithms with optimized performance: (i) the SAPCo Sort algorithm as a parallel counting sort algorithm that is faster than comparison-based sorting algorithms in degree-ordering of power-law graphs, (ii) the iHTL algorithm that optimizes locality in Sparse Matrix-Vector (SpMV) Multiplication graph algorithms by extracting dense subgraphs containing incoming edges to in-hubs and processing them in the push direction, and (iii) the LOTUS algorithm that optimizes locality in Triangle Counting by separating different caching demands and deploying specific data structure and algorithm for each of them.

Bibtex

@phdthesis{ODSAGA-ethos.874822,
  title  = {On Designing Structure-Aware High-Performance Graph Algorithms},
  author = {Mohsen Koohi Esfahani},
  year   = 2022,
  url    = {https://blogs.qub.ac.uk/DIPSA/On-Designing-Structure-Aware-High-Performance-Graph-Algorithms-PhD-Thesis/},
  school = {Queen's University Belfast},
  EThOSID = {uk.bl.ethos.874822}
}

Related Posts

LaganLighter

LaganLighter Source Code

Posted on by
Reply


Repository

https://github.com/DIPSA-QUB/LaganLighter

Documentation

https://github.com/DIPS-QUB/LaganLighter/tree/main/docs

Algorithms in This Repo

Cloning

git clone https://github.com/MohsenKoohi/LaganLighter.git --recursive

Graph Types

LaganLighter supports the following graph formats:

  • CSR/CSC graph in text format, for testing. This format has 4 lines: (i) number of vertices (|V|), (ii) number of edges (|E|), (iii) |V| space-separated numbers showing offsets of the vertices, and (iv) |E| space-separated numbers indicating edges.
  • CSR/CSC WebGraph format: supported by the Poplar Graph Loading Library
    external git repository

Measurements

In addition to execution time, we use the PAPI library to measure hardware counters such as L3 cache misses, hardware instructions, DTLB misses, and load and store memory instructions. ( papi_(init/start/reset/stop) and (print/reset)_hw_events functions defined in omp.c).

To measure load balance, we measure the total time of executing a loop and the time each thread spends in this loop (mt and ttimes in the following sample code). Using these values, PTIP macro (defined in omp.c) calculates the percentage of average idle time (as an indicator of load imbalance) and prints it with the total time (mt). 

mt = - get_nano_time()
#pragma omp parallel  
{
   unsigned tid = omp_get_thread_num();
   ttimes[tid] = - get_nano_time();
	
   #pragma omp for nowait
   for(unsigned int v = 0; v < g->vertices_count; v++)
   {
      // .....
   }
   ttimes[tid] += get_nano_time();
}
mt += get_nano_time();
PTIP("Step ... ");

As an example, the following execution of Thrifty, shows that the “Zero Planting” step has been performed in 8.98 milliseconds and with a 8.22% load imbalance, while processors have been idle for 72.22% of the execution time, on average, in the “Initial Push” step.

NUMA-Aware and Locality-Preserving Partitioning and Scheduling

In order to assign consecutive partitions (vertices and/or their edges) to each parallel processor, we initially divide partitions and assign a number of consecutive partitions to each thread. Then, we specify the order of victim threads in the work-stealing process. During the initialization of LaganLighter parallel processing environment (in initialize_omp_par_env() function defined in file omp.c), for each thread, we create a list of threads as consequent victims of stealing.

A thread, first, steals jobs (i.e., partitions) from consequent threads in the same NUMA node and then from the threads in consequent NUMA nodes. As an example, the following image shows the stealing order of a 24-core machine with 2 NUMA nodes. This shows that thread 1 steals from threads 2, 3, …,11, and ,0 running on the same NUMA socket and then from threads 13, 14, …, 23, and 12 running on the next NUMA socket.

We use dynamic_partitioning_...() functions (in file partitioning.c) to process partitions by threads in the specified order. A sample code is in the following:

struct dynamic_partitioning* dp = dynamic_partitioning_initialize(pe, partitions_count);

#pragma omp parallel  
{
   unsigned int tid = omp_get_thread_num();
   unsigned int partition = -1U;		

   while(1)
   {
      partition = dynamic_partitioning_get_next_partition(dp, tid, partition);
      if(partition == -1U)
	 break; 

      for(v = start_vertex[partition]; v < start_vertex[partition + 1]; v++)
      {
	// ....
       }
   }
}

dynamic_partitioning_reset(dp);

Bugs & Support

As “we write bugs that in particular cases have been tested to work correctly”, we try to evaluate and validate the algorithms and their implementations. If you receive wrong results or you are suspicious about parts of the code, please contact us or submit an issue.

License

Licensed under the GNU v3 General Public License, as published by the Free Software Foundation. You must not use this Software except in compliance with the terms of the License. Unless required by applicable law or agreed upon in writing, this Software is distributed on an “as is” basis, without any warranty; without even the implied warranty of merchantability or fitness for a particular purpose, neither express nor implied. For details see terms of the License.

Copyright 2022 The Queen’s University of Belfast, Northern Ireland, UK

LaganLighter

Related Posts

Technical Posts

MASTIFF: Structure-Aware Minimum Spanning Tree/Forest – ICS’22

Posted on by
Reply

36th ACM International Conference on Supercomputing 2022
June 27-30, 2022
Acceptance Rate: 25%

DOI: 10.1145/3524059.3532365
Authors’ Copy (PDF Format)

The Minimum Spanning Forest (MSF) problem finds usage in many different applications. While theoretical analysis shows that linear-time solutions exist, in practice, parallel MSF algorithms remain computationally demanding due to the continuously increasing size of data sets.

In this paper, we study the MSF algorithm from the perspective of graph structure and investigate the implications of the power-law degree distribution of real-world graphs
on this algorithm.

We introduce the MASTIFF algorithm as a structure-aware MSF algorithm that optimizes work efficiency by (1) dynamically tracking the largest forest component of each graph component and exempting them from processing, and (2) by avoiding topology-related operations such as relabeling and merging neighbour lists.

The evaluations on 2 different processor architectures with up to 128 cores and on graphs of up to 124 billion edges, shows that Mastiff is 3.4–5.9× faster than previous works.

Code Availability
The source-code of MASTIFF is available on LaganLighter Repository (alg3_mastiff.c and msf.c files). A sample execution of this source code for “Twitter-MPI” graph is shown in the following:

BibTex

@INPROCEEDINGS{10.1145/3524059.3532365,
author = {Koohi Esfahani, Mohsen and Kilpatrick, Peter and Vandierendonck, Hans},
title = {{MASTIFF}: Structure-Aware Minimum Spanning Tree/Forest},
year = {2022},
isbn = {},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
url = {https://doi.org/10.1145/3524059.3532365},
doi = {10.1145/3524059.3532365},
booktitle = {Proceedings of the 36th ACM International Conference on Supercomputing},
numpages = {13}
}

LaganLighter

Related Posts