Tag Archives: pushpull

Locality Analysis of Graph Reordering Algorithms – IISWC’21

Posted on by

2021 IEEE International Symposium on Workload Characterization (IISWC’21)
November 7-9, 2021
Acceptance Rate: 39.5%
DOI: 10.1109/IISWC53511.2021.00020

Authors’ Copy (PDF Format)

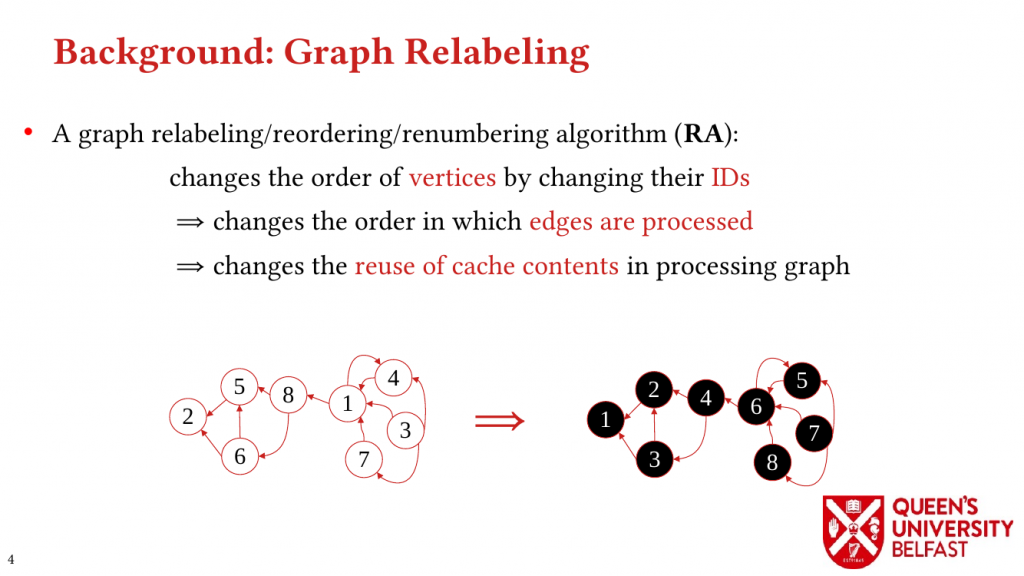
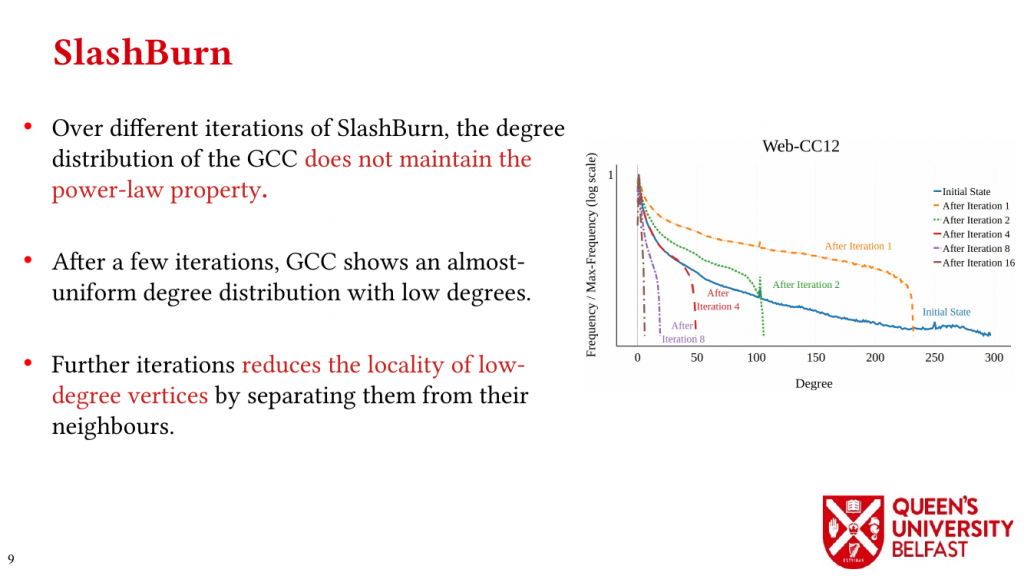
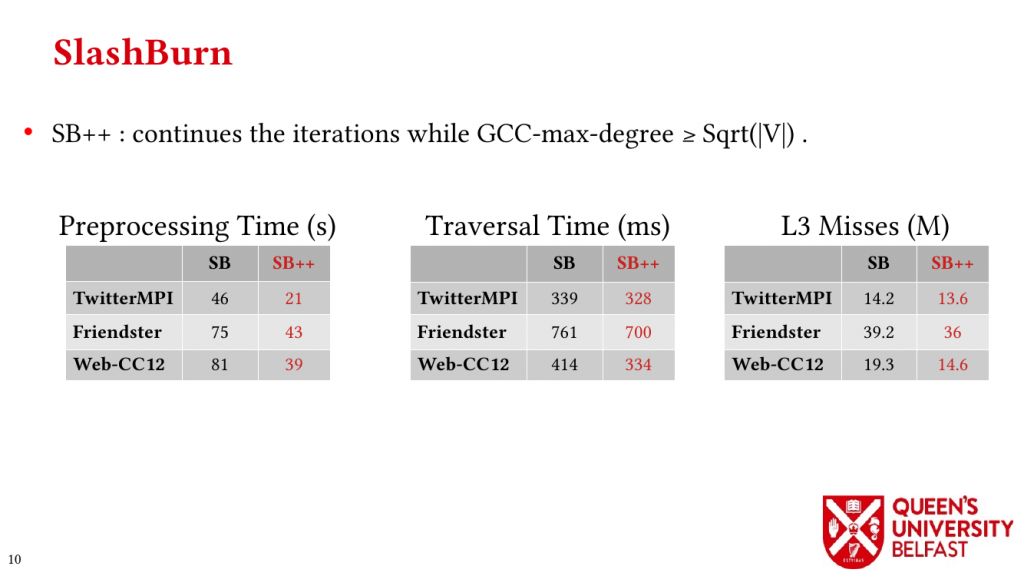
Graph reordering algorithms try to improve locality of graph algorithms by assigning new IDs to vertices that ultimately changes the order of random memory accesses. While graph relabeling algorithms such as SlashBurn, GOrder, and Rabbit-Order provide better locality, it is not clear how they affect graph processing and different graph datasets , mainly, for three reasons:
(1) The large size of datasets,
(2) The lack of suitable measurement tools, and
(3) Disparate characteristics of graphs.
The paucity of analysis has also inhibited the design of more efficient RAs.

This paper introduces a number of metrics and tools to investigate the functionality of graph reordering algorithms and their effects on different real-world graph datasets:
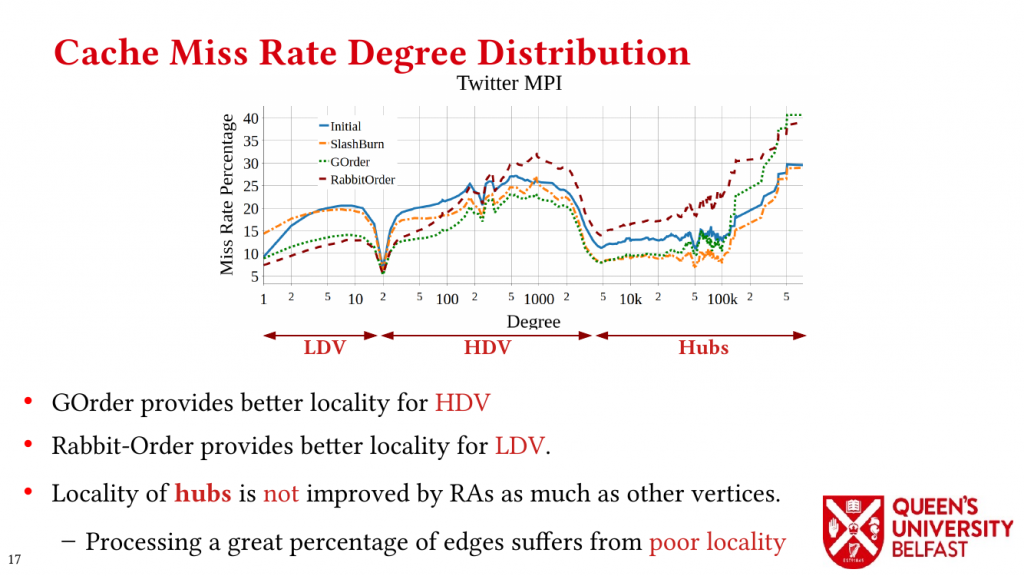
(1) We introduce the Cache Miss Rate Degree Distribution and Degree Distribution of Neighbour to Neighbour Average Distance ID (N2N AID) to show how reordering algorithms affect different vertices,
(2) We introduce the Effective Cache Size as a metric to measure how much of cache capacity is used by reordered graphs for satisfying random memory accesses,
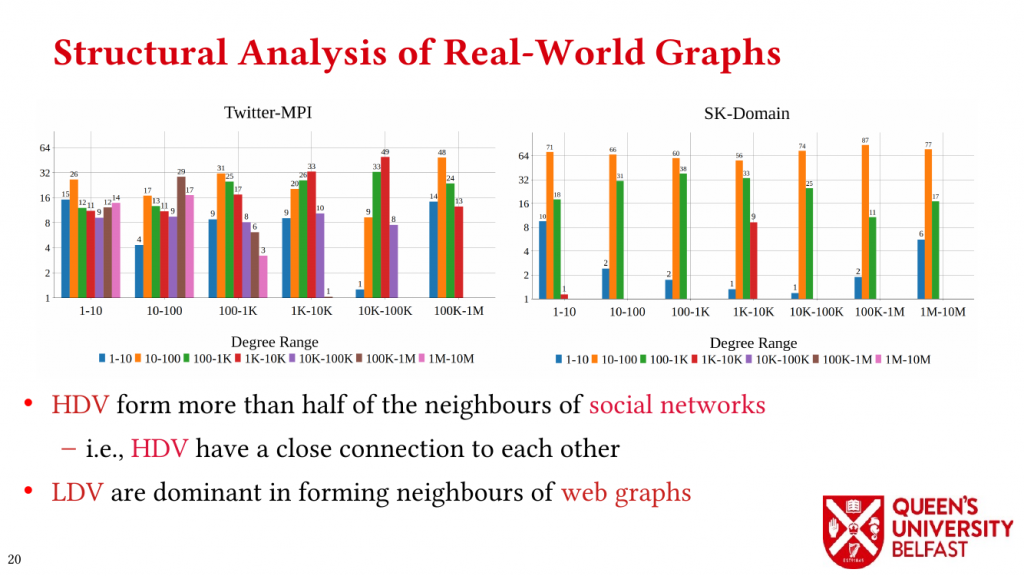
(3) We introduce the Assymetricity Degree Distribution and Neighbourhood Decomposition to explain the composition of neighbourhood of vertices to explain structural differences between web graphs and social networks.
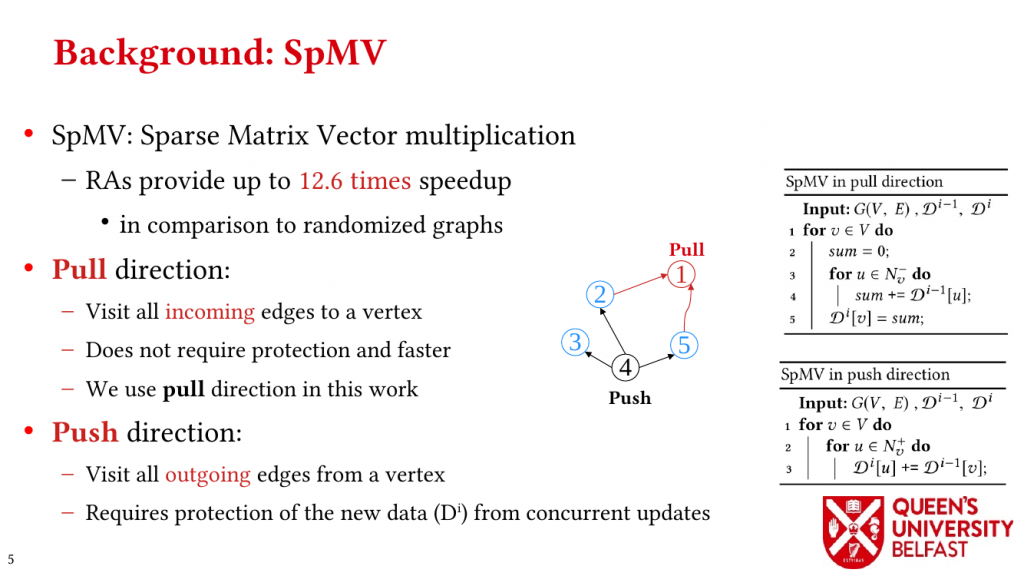
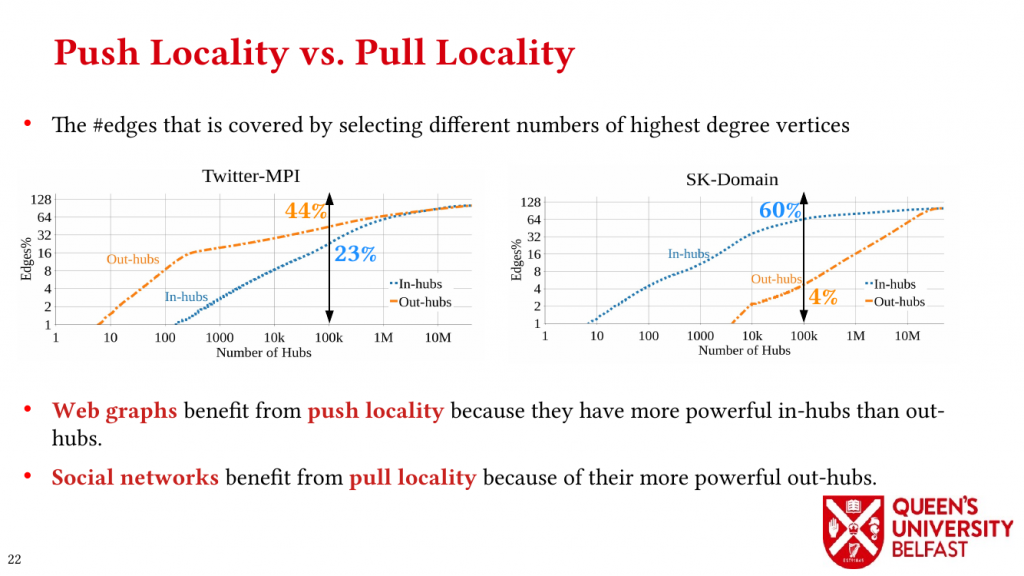
(4) We investigate the effects of the structure of real-world graphs on the locality and performance of traversing graphs in pull and push directions by introducing Push Locality and Pull Locality.

Finally, we present improvements to graph reordering algorithms and propose other suggestions based on the new insights and features of real-world graphs introduced by this paper.

BibTex

@INPROCEEDINGS{10.1109/IISWC53511.2021.00020,
  author={Koohi Esfahani, Mohsen and Kilpatrick, Peter and Vandierendonck, Hans},
  booktitle={2021 IEEE International Symposium on Workload Characterization (IISWC'21)},  
  title={Locality Analysis of Graph Reordering Algorithms}, 
  year={2021},
  volume={},
  number={},
  pages={101-112},
  publisher={IEEE Computer Society},
  doi={10.1109/IISWC53511.2021.00020}
}

Related Posts

LaganLighter

Thrifty Label Propagation: Fast Connected Components for Skewed-Degree Graphs – IEEE CLUSTER’21

Posted on by
IEEE CLUSTER 2021

IEEE CLUSTER 2021
7-10 September
Acceptance rate: 29.4%

DOI: 10.1109/Cluster48925.2021.00042
IEEE Xplore
PDF Version (Authors’ Copy)

Thrifty introduces four optimization techniques to Label Propagation Connected Components:

1) Unified Labels Array accelerates label propagation by allowing the latest label of each vertex to be read in processing other vertices.

2) Zero Convergence optimizes work-efficiency in the pull iterations of Label Propagation by skipping converged vertices.

3) Zero Planting selects the best start propagating point and increases the convergence rate and removes pull iterations that are required for the lowest label to reach the core of graph.

4) Initial Push technique makes the first iteration work efficient by skipping processing edges of vertices that probability of convergence is very small.

Based on these optimizations, Thrifty provides 1.4✕ speedup to Afforest, 6.6✕ to Jayanti-Tarjan, 14.3✕ to BFS-CC, and 25.0✕ to Direction Optimizing Label Propagation.

  • Thrifty Label Propagation: Fast Connected Components For Skewed Degree Graphs
  • Thrifty Label Propagation: Outline
  • Thrifty Label Propagation: Background
  • Thrifty Label Propagation: Background
  • Thrifty Label Propagation: Background
  • Thrifty Label Propagation
  • Thrifty Label Propagation: Unified Labels Array
  • Thrifty Label Propagation: Unified Labels Array
  • Thrifty Label Propagation: Zero Convergence
  • Thrifty Label Propagation: Zero Convergence
  • Thrifty Label Propagation: Zero Planting
  • Thrifty Label Propagation: Zero Planting
  • Thrifty Label Propagation: Initial Push
  • Thrifty Label Propagation: Evaluation
  • Thrifty Label Propagation: Evaluation
  • Thrifty Label Propagation: Evaluation
  • Thrifty Label Propagation: Conclusion
  • Thrifty Label Propagation: Thanks
  • Thrifty Label Propagation: A Gift from QUB


Code Availability
The source-code of Thrifty is available on LaganLighter Repository (alg2_thrifty.c and cc.c files). A sample execution of this source code for “Twitter-MPI” graph is shown in the following:


Bibtex

@INPROCEEDINGS{10.1109/Cluster48925.2021.00042,
  author={Koohi Esfahani, Mohsen and Kilpatrick, Peter and Vandierendonck, Hans},
  booktitle={2021 IEEE International Conference on Cluster Computing (CLUSTER)}, 
  title={Thrifty Label Propagation: Fast Connected Components for Skewed-Degree Graphs}, 
  year={2021},
  volume={},
  number={},
  pages={226-237},
  publisher={IEEE Computer Society},
  doi={10.1109/Cluster48925.2021.00042}
}

Related Posts

Exploiting in-Hub Temporal Locality in SpMV-based Graph Processing – ICPP’21

Posted on by
ICPP'21

50th International Conference on Parallel Processing (ICPP’21)
August 9-12, 2021
Acceptance Rate: 26.4%

DOI:10.1145/3472456.3472462
ACM Digital Library
PDF Version (Authors’ Copy)

This paper investigates the implications made by the structure of real-world graphs with power-law degree distribution on the locality of SpMV graph analytics, and by considering the efficacy of locality optimizing graph reordering algorithms (such as SlashBurn, GOrder, and Rabbit-Order) shows that irregular datasets requires special traversals in order to improve locality for hub vertices that dedicate a large portion of the processing time to themselves.

We introduce in-Hub Temporal Locality (iHTL) as a structure-aware and cache-friendly graph traversal that optimizes locality in pull traversal. iHTL identifies different blocks in the adjacency matrix of a graph and applies a suitable traversal direction (push or pull) for each block based on its contents. In other words, iHTL optimizes locality of one traversal of all edges of the graph by:

(1) applying push direction for flipped blocks containing edges to in-hubs, and
(2) applying pull direction for processing sparse block containing edges to non-hubs.

Moreover, iHTL introduces a new algorithm to efficiently identify the number of flipped blocks by investigating connection between hub vertices of the graph. This allows iHTL to create flipped blocks as much as the graph structure requires and makes iHTL suitable for a wide range of different real-world graph datasets like social networks and web graphs.

iHTL is 1.5× – 2.4× faster than pull and 4.8× – 9.5× faster than push in state-of-the-art graph processing frameworks. More importantly, iHTL is 1.3× – 1.5× faster than pull traversal of state-of-the-art locality optimizing reordering algorithms such as SlashBurn, GOrder, and Rabbit-Order while reduces the preprocessing time by 780×, on average.

  • Exploiting in-Hub Temporal Locality in SpMV-based Graph Processing
  • Exploiting in-Hub Temporal Locality in SpMV-based Graph Processing : Outline
  • Exploiting in-Hub Temporal Locality in SpMV-based Graph Processing : Introduction
  • Exploiting in-Hub Temporal Locality in SpMV-based Graph Processing : Pull vs Push
  • Exploiting in-Hub Temporal Locality in SpMV-based Graph Processing : Is Pull A Suitable Direction
  • Exploiting in-Hub Temporal Locality in SpMV-based Graph Processing : iHTL: in-Hub Temporal Locality
  • Exploiting in-Hub Temporal Locality in SpMV-based Graph Processing : iHTL Graph Structure
  • Exploiting in-Hub Temporal Locality in SpMV-based Graph Processing : SpMV in iHTL
  • Exploiting in-Hub Temporal Locality in SpMV-based Graph Processing : Evaluation
  • Exploiting in-Hub Temporal Locality in SpMV-based Graph : Conclusion
  • Exploiting in-Hub Temporal Locality in SpMV-based Graph : Thanks
  • Exploiting in-Hub Temporal Locality in SpMV-based Graph : A Gift From QUB

Code Availability
The source-code will be published soon.

BibTex


@INPROCEEDINGS{10.1145/3472456.3472462,
author = {Koohi Esfahani, Mohsen and Kilpatrick, Peter and Vandierendonck, Hans},
title = {Exploiting In-Hub Temporal Locality In SpMV-Based Graph Processing},
year = {2021},
isbn = {9781450390682},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
url = {https://doi.org/10.1145/3472456.3472462},
doi = {10.1145/3472456.3472462},
booktitle = {50th International Conference on Parallel Processing},
numpages = {10},
location = {Lemont, IL, USA},
series = {ICPP 2021}
}

LaganLighter

Related Posts

Graptor: Efficient Pull and Push Style Vectorized Graph Processing

Posted on by

https://doi.org/10.1145/3392717.3392753

Vectorization seeks to accelerate computation through data-level parallelism. Vectorization has been applied to graph processing, where the graph is traversed either in a push style or a pull style. As it is not well understood which style will perform better, there is a need for both vectorized push and pull style traversals. This paper is the first to present a general solution to vectorizing push style traversal. It more-over presents an enhanced vectorized pull style traversal.

Our solution consists of three components: CleanCut, a graph partitioning approach that rules out inter-thread race conditions; VectorFast, a compact graph representation that supports fast-forwarding through the edge stream; and Graptor, a domain-specific language and compiler for auto-vectorizing and optimizing graph processing codes.

Experimental evaluation demonstrates average speedups of 2.72X over Ligra, 2.46X over GraphGrind, and 2.33X over GraphIt. Graptor outperforms Grazelle, which performs vectorized pull style graph processing, by 4.05 times.

    The GraphGrind Framework: Fast Graph Analytics on Large Shared-Memory Systems (PhD Thesis)

    Posted on by

    Thesis on QUB Pure Portal
    Thesis in PDF Format

    Author: Jiawen Sun, https://www.linkedin.com/in/jiawen-sun-33b368103/

    As shared memory systems support terabyte-sized main memory, they provide an opportunity to perform efficient graph analytics on a single machine. Graph analytics is characterised by frequent synchronisation, which is addressed in part by shared memory systems. However, performance is limited by load imbalance and poor memory locality, which originate in the irregular structure of small-world graphs.
    This dissertation demonstrates how graph partitioning can be used to optimise (i) load balance, (ii) Non-Uniform Memory Access (NUMA) locality and (iii) temporal locality of graph partitioning in shared memory systems. The developed techniques are implemented in GraphGrind, a new shared memory graph analytics framework.

    At first, this dissertation shows that heuristic edge-balanced partitioning results in an imbalance in the number of vertices per partition. Thus, load imbalance exists between partitions, either for loops iterating over vertices, or for loops iterating over edges. To address this issue, this dissertation introduces a classification of algorithms to distinguish whether they algorithmically benefit from edge-balanced or vertex-balanced partitioning. This classification supports the adaptation of partitions to the characteristics of graph algorithms. Evaluation in GraphGrind, shows that this outperforms state-of-the-art graph analytics frameworks for shared memory including Ligra by 1.46x on average, and Polymer by 1.16x on average, using a variety of graph algorithms and datasets.

    Secondly, this dissertation demonstrates that increasing the number of graph partitions is effective to improve temporal locality due to smaller working sets.
    However, the increasing number of partitions results in vertex replication in some graph data structures. This dissertation resorts to using a graph layout that is immune to vertex replication and an automatic graph traversal algorithm that extends the previously established graph traversal heuristics to a 3-way graph layout choice is designed. This new algorithm furthermore depends upon the classification of graph algorithms introduced in the first part of the work. These techniques achieve an average speedup of 1.79x over Ligra and 1.42x over Polymer.

    Finally, this dissertation presents a graph ordering algorithm to challenge the widely accepted heuristic to balance the number of edges per partition and minimise edge or vertex cut. This algorithm balances the number of edges per partition as well as the number of unique destinations of those edges. It balances edges and vertices for graphs with a power-law degree distribution. Moreover, this dissertation shows that the performance of graph ordering depends upon the characteristics of graph analytics frameworks, such as NUMA-awareness. This graph ordering algorithm achieves an average speedup of 1.87x over Ligra and 1.51x over Polymer.